
dBmというものが一体何なのか、全然わからないという方は、ぜひ本記事を読んで頂きたいです。本記事は、そんな悩みを持っている方のために書きました。dBmの読み方などの初歩的な知識からはじめ、次に、数学的にどのような意味があるのかを簡単かつわかりやすく説明します。そして最後に、なぜ無線電力をdBmで表現するとよいのか、ということを説明します。これらのことが迷わずしっかり理解できるように、短い文章に区切って説明しています。本記事を読んで頂ければ、数字・通信技術・回路に詳しくない方でもdBmについて正確に意味を理解でき、それに伴い、dBmで表現された無線機器の性能がはっきりイメージできるようになります。
単位「dBm」とは?
dBmとは電力をより少ない桁数で表したものです。0dBmが1mWを表しています。数学的に表現すると、『10を底とした対数』です。これはどういうことかというと、『10の何乗なのか』という意味です。
dBmは「電力強度」の単位
無線LAN(Wi-Fi)の電力強度を表す単位として、dBmが利用されています。任意の値として例えば10dBmと記載されている場合、電力を表しており、0dBm=1mWからどの程度違うのかを示します。10dBmは10mWですが、20dBmは20mWではありません。不思議ですね!なぜそうなるのか、1つずつ解説していきます。
「受信感度」の単位としても
通信技術の「受信感度」もdBmを使います。これは、「公称の誤り性能を満たすことができる最小の受信電力」を表しています。つまり、Wi-Fiなどの無線用アンテナが、電波の信号を間違えずにきちんと理解できる限界の値ということです。そのため、非常に小さな値になります。一般に、後述する負のdBmで示します。
通信技術、アプリケーション、電気回路、情報の送信といった場面で使用されます。
読み方
読み方は、『ディー・ビー・エム』です。『デシベル・ミリワット』が正式な呼称なのですが、長いので、実際にはほとんど前者が使われます。
定義「0dBm」は1mW
電波強度や受信感度を表す単位は、電力の単位である「mW(ミリワット)」「W(ワット)」で表しますが、1mWは「0dBm」と定義されています。0dBmは電力が0(ない)と考えてしまいそうですが、dBmは2つの値を比較して表現する単位なので、電波強度が0にはなりません。マイナスの値にもなる点に注意したいです。
dBmで表現するメリット
なぜdBmを使うのかを説明するには、少しだけ数学的な説明が必要になるので、根気よく読んで頂く必要があります。まず、dBmは、mWを10の何条倍かで表しています。例えば、20dBは100mW、30dBは1000mW、-20dBは100分の1mWを表しています。
10dBmは10mWになりますが、20dBmは10の2乗倍を表すため、20dBmは100mWになります。ややこしいですが、電波強度は大きな値になるため、少ない数字で大きな数を表現するのが、dBmを使うメリットになります。
dBmの目安(無線LAN・Wi-Fi・スマホ)
無線LAN・Wi-Fi・スマホのdBmで十分な通信速度を出す目安は以下のように言われています。
2.4GHz→-65dBm以上
5Ghz→-60dBm以上
接続が不安定にならないためには少なくとも-75dBm以上のdBmは必要と言われます。
dBmと似た用語もあります。
mbpsは以下で解説しています。

pingは以下で解説しています。


mtuは以下で解説しています。

電波強度「dBm」はなぜマイナスになる?理由をわかりやすく

電波強度や光の受信感度を表す「dBm」はマイナスの値にもなります。しかし、dBwとは0dBm=「1mW」と比較して何倍(何分の一)になったかを比較する単位なので、dBmがマイナスや0の値をとっても、電波強度や受信感度はマイナスや0にはなることはなく、必ず正の値をとります。
【マイナス編】dBmとmWの変換
特に難しいのがマイナスのつくdBmの変換です。変換式は上が使えますがマイナス〇の数字が大きくなるほどイメージが難しくなります。
例としてマイナスのdBmとmWの換算を挙げます。
かなり数値が小さくなるのでマイクロワットuW(1uW=0.001mW)、ナノワットnW(1nW=0.000001mW)、ピコワットpW(1pW=0.000000001mW)が登場します。
| -29dbm | 1.259uW |
| -38dbm | 316.228nW |
| -60dbm | 1000pW |
| -62dbm | 630.957pW |
| -66dbm | 251.189pW |
| -83dbm | 5.012pW |
| -88dbm | 1.585pW |
| -108dbm | 0.0158pW |
| -110dbm | 0.01pW |
dBmとmWの違いと変換・計算式
dBmとmWの違いや変換方法を解説していきます。やはりここでも数学が関係しているため、説明がやや複雑になるので、順を追って少しずつ進んで行きましょう。
・dBmとmWの違い
dBmとmWの違いは簡単です。mWは現実の電力値そのままです。それに対してdBmは、後述する数式によって変換された、『対数』というものです。
・対数はどんな場面で有益なのか?
対数がどんな場面で有益なのかというと、『急激な変化率を持つ値を扱う場合です。これはすなわち、『指数関数的に変化する値』です。
・指数関数とは?
指数関数とは、簡単に書くと『Y=AX^B』の形で表される数の集まりです。これは、Xが増大するにつれて爆発的にYが増大するという性質があります。ということは、大きなXを扱うときに計算が大変になってしまうという弱点があります。
・指数関数を対数にするとどうなる?
指数関数を対数に変換するとどうなるでしょうか?実は、対数関数は指数関数のグラフに対して『Y=Xの直線に対して対称』という性質があります。それはつまり、『Xが増大していってもYがあまり増大しない』形になることを意味します。ということは、『計算がとても簡単になる』ということなのです!!
・なぜ電波に対してdBを使うの?
なぜ電波に対してdBを使うのかというと、先述した扱う桁数が減るという利点に加えて、伝送路全体の利得計算が簡単になるからです。電波を送受信するシステムは、複数の増幅点・減衰点があります。その利得計算が簡単な足し算・引き算の繰り返しでできるというのは、伝送路設計の現場において、とても効率が良いのです。
dB(デシベル)とdBm(デシベルミリワット)の違いや計算・換算表
dBとdBmの違いや計算・換算表を紹介していきましょう。
dB(デシベル)とdBm(デシベルミリワット)の違い
dBmと似た単位に「dB(デシベル)」があります。dBとdBmは似ていますが、違う単位です。
dBwは1mWを基準とした「電力」を表す単位です。
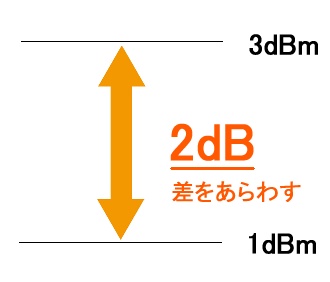
dBは電力の増幅幅(差)を表す単位になります。増幅幅とは何のことわかりにくいですが、〇dBmから△dBmに増えた(減った)場合の2つの値の「差」のことです。
数字が、1から3に増加するとき、差は2になります。
3から5に増加するときも差は2です。この2にあたる数値がdBです。
「〇dB」という表現は、2つのdBmの差を表していますが、
どこから変化するか(1か3か)で増加後の3と5は変わることがわかります。
dBは電力の足し算・引き算で使用され
以下の式が成り立ちます。
[dBm]+[dB]=[dBm]
[dBm]-[dB]=[dBm]
[dBm]-[dBm]=[dB]
デシベルの足し算
デシベルの足し算は、基準値1mWを何倍するかを表しています。
デシベルは差を表す単位ですが、dBmが「〇倍」を表現していると話しましたので、
結果的にdBmの差=mWが何倍かを表します。
・計算例: 0dBm+10dB=10dBm=10mW
【計算式】変換・換算方法
変換・換算方法を紹介しましょう。以下の計算式によって、電力値をデシベル表現に換算することができます。
10 ✖ log10 (出力電力 ÷ 入力電力)
基準となる入力電力は、1mWです。例えば、1000mWをデシベルに変換する場合、『10✖log10(1000÷1)=10✖3=30dB』となります。結果は、『出力と入力の比が、10の何乗で表せるか』、という意味です。これを加算・減算するということは、『何乗になるか』の部分を増減して決定しているので、倍率を操作していることになり、乗算・除算の変わりができるわけです。
10dBは何倍?
10dbは何倍かというと、10倍になります。-10dBになると、10分の1倍になります。再度述べますが、このdBという値は、dBmに対して加算・減算してよいという法則があります。
・計算例:10✖log10(10÷1)=10✖1=10dB
10dB・20dB・30dB(デシベル)は何倍?
10dB・20dB・30dB(デシベル)は何倍になるのでしょうか。
以下のようになります。
10dB→10倍
20dB→100倍
30dB→1000倍
dBがマイナス?
dBがマイナスの場合、それを基準値に加算(=減算)することは、基準値1mWを除して小さな値にすることを表しています。例えば、10分の1など、基準値より少なくなる場合に、マイナスで表現します。
・計算例: 0dBm-10dB=-10dBm=0.1mW
dBの計算式と換算表
計算式と対応表を以下に掲載します。これを見ると、dBをすぐに実際の電力値に変換できて便利です!
| デシベル(dB) | 電力・音響パワー等
の倍率 |
| -6デシベル | 0.25倍 |
| -5デシベル | 0.32倍 |
| -4デシベル | 0.40倍 |
| -3デシベル | 0.50倍 |
| -2デシベル | 0.63倍 |
| -1デシベル | 0.79倍 |
| 0デシベル | 1.00倍 |
| 0.1デシベル | 1.02倍 |
| 0.25デシベル | 1.06倍 |
| 0.5デシベル | 1.12倍 |
| 0.75デシベル | 1.19倍 |
| 1デシベル | 1.26倍 |
| 2デシベル | 1.58倍 |
| 3デシベル | 2.00倍 |
| 4デシベル | 2.51倍 |
| 5デシベル | 3.16倍 |
| 6デシベル | 3.98倍 |
| 7デシベル | 5.01倍 |
| 8デシベル | 6.31倍 |
| 9デシベル | 7.94倍 |
| 10デシベル | 10.00倍 |
| 20デシベル | 100.00倍 |
| 30デシベル | 1000.00倍 |
| 40デシベル | 10000.00倍 |
| 50デシベル | 100000.00倍 |
| 100デシベル | 10000000000倍 |
まとめ
電波の強さを表すのにdBmを使用します。これはdBを加算・減算することで簡単に計算できます。本記事では、dBmの意味と計算上の仕組みについて、できるだけシンプルになるよう心がけて解説してきました。指数関数と対数関数の関係がわかると、とても理解しやすいですね。そこから実務上の計算の面倒さに思い至れば、なぜ電波の電力を表現するのにdBmを使うのか、明確に理解できますね。これで、dBmについてもう迷うことがなくなり、誰かに質問されても自信をもって答えることができるようになったのではないでしょうか!そして、アンテナの性能がはっきりイメージできるようになったはずです。わかってしまえばとても単純明快なことだったのです。身近な人がdBmやdBで迷っているのを見つけたら、ぜひ本記事を参考に、優しく丁寧に解説してあげてください。